






A、试题类型:
送分题。
B、算法模型:
无。
C、试题说明:
读题。
#include<iostream>
using namespace std;
int n, a[200], b[200],na,nb,c,d;
void initialize()
{
int i;
cin >> n >> na >> nb;
for (i = 0; i < na; i++)
cin >> a[i];
for (; i < n; i++)
a[i] = a[i - na];
for (i = 0; i < nb; i++)
cin >> b[i];
for (; i < n; i++)
b[i] = b[i - nb];
}
void compare(int x,int y)
{
switch (x)
{
case 0:
switch (y)
{
case 1:
case 4:d++; break;
case 2:
case 3:c++; break;
}
break;
case 1:
switch (y)
{
case 2:
case 4:d++; break;
case 0:
case 3:c++; break;
}
break;
case 2:
switch (y)
{
case 0:
case 3:d++; break;
case 1:
case 4:c++; break;
}
break;
case 3:
switch (y)
{
case 1:
case 0:d++; break;
case 2:
case 4:c++; break;
}
break;
case 4:
switch (y)
{
case 2:
case 3:d++; break;
case 0:
case 1:c++; break;
}
}
}
void operate()
{
for (int i = 0; i < n; i++)
compare(a[i], b[i]);
}
void show()
{
cout << c << ' ' << d;
}
int main()
{
initialize();
operate();
show();
return 0;
}
A、试题类型:
结构与算法。
B、算法模型:
暴力dfs,暴力hash。
C、试题说明:
树编程。
int s=0;
for(int i=1;i<=k;i++)
{
sum=(sum+s*r[i])%P;
s=(s+r[i])%P;
}
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#define P 10007
#define M 2000005
using namespace std;
struct link
{
int u,v,w;
}l[M];
int n,t,ans,sum,r[M],w[M];
bool com(link a,link b)
{
return a.u>b.u;
}
void work(int k)
{
int s=0;
for(int i=1;i<=k;i++)
{
sum=(sum+s*r[i])%P;
s=(s+r[i])%P;
}
int mx1=0,mx2=0,x=0;
for(int i=1;i<=k;i++)
{
if(r[i]>mx1)
{
mx1=r[i];
x=i;
}
}
for(int i=1;i<=k;i++)
if(i!=x)mx2=max(mx2,r[i]);
ans=max(ans,mx1*mx2);
}
int main()
{
cin>>n;
for(int i=1;i<n;i++)
{
scanf("%d%d",&l[i*2].u,&l[i*2].v);
l[i*2-1].v=l[i*2].u;
l[i*2-1].u=l[i*2].v;
}
for(int i=1;i<=n;i++)scanf("%d",&w[i]);
sort(l+1,l+2*n+1,com);
int j=0;
for(int i=1;i<=2*n;i++)
{
if(i==1||l[i].u==l[i-1].u)
r[++j]=w[l[i].v];
else
{
work(j);
j=0;
r[++j]=w[l[i].v];
}
}
work(j);
sum=(sum*2)%P;
cout<<ans<<' '<<sum;
}
A、试题类型:
生活应用。
B、算法模型:
背包问题与方程不等式。
C、试题说明:
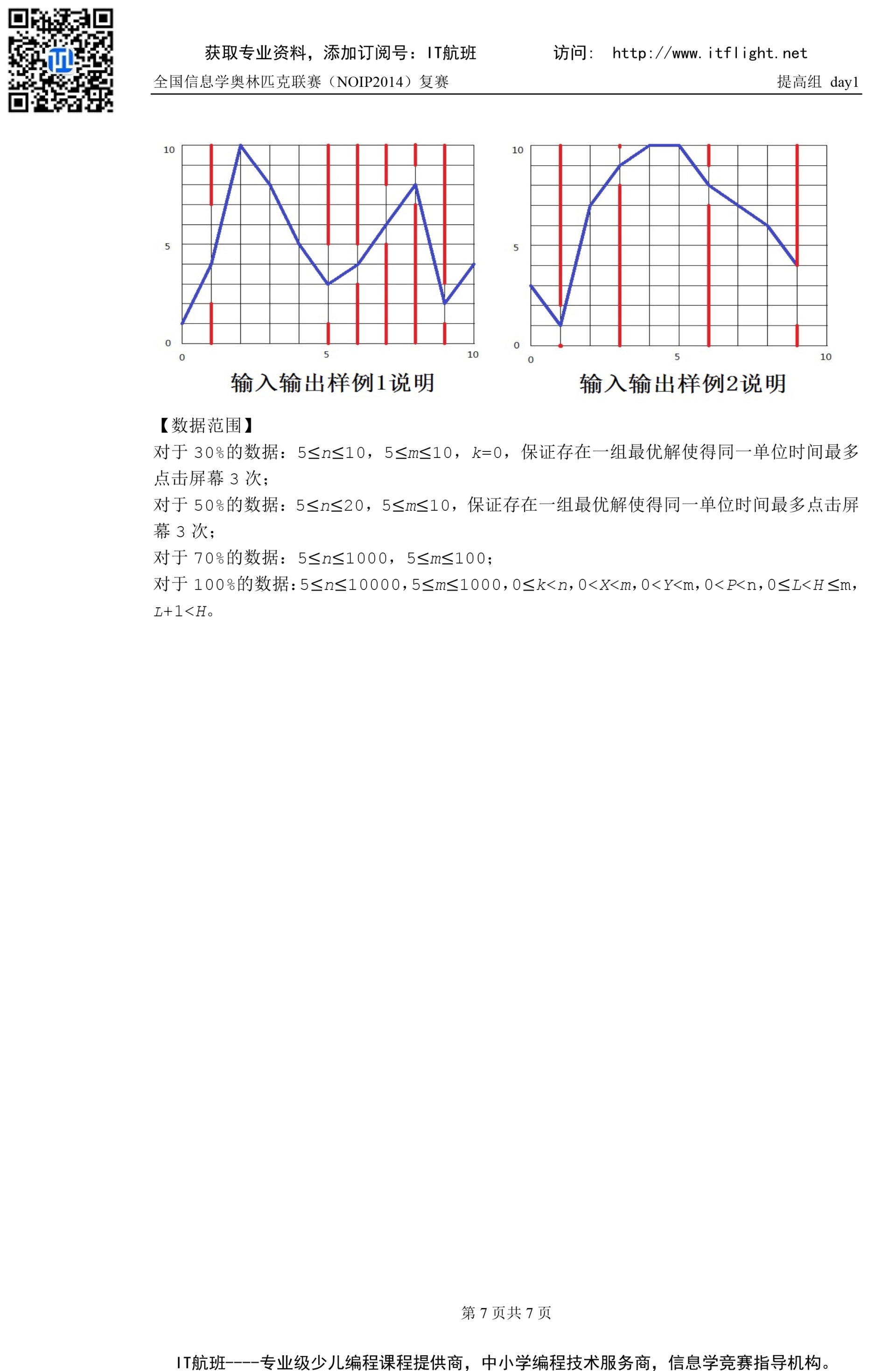
读完题可以发现,每次点击可以分为两种背包,向上为完全背包,向下为0/1背包,那么就可以把每一个横坐标的答案分为两个背包来求解。
f[i][j]表示坐标为(i,j)的点最少需要多少次。
转移方程为:f[i][j]=min(f[i-1][j-up[i]*k]+k)。
这样做的效率为n^3的,肯定没有分数。
考虑优化,发现f[i][j-up[i]*k]+k可以从f[i][j-up[i]*(k-1)]+k-1转移。
所以转移方程变为:f[i][j]=min(f[i-1][j-up[i]])。
最后注意到达m是不能继续向上飞的条件。
#include<bits/stdc++.h>
using namespace std;
const int max_n = 10010;
const int max_m = 1010;
const int inf = 1e9+7;
struct node
{
int pos,l,h;
}a[max_n];
int f[2][max_m],up[max_n],down[max_n];
int n,m,t,num=1,ans=inf,k;
inline bool cmp(node a,node b)
{
return a.pos<b.pos;
}
inline void dp()
{
int tmp=0;
for(int i=1; i<=n; ++i)
{
tmp^=1;
for(int j=0; j<=m; ++j)
f[tmp][j]=inf+m;
for(int j=up[i]+1; j<=m; ++j)
f[tmp][j]=min(f[tmp][j],min(f[tmp^1][j-up[i]]+1,f[tmp][j-up[i]]+1));
for(int j=up[i]+1; j<=m; ++j)
if(i==a[num].pos && !(j>a[num].l && j<a[num].h)) f[tmp][j]=inf+m;
for(int j=m-up[i]; j<=m; ++j)
f[tmp][m]=min(f[tmp][m],min(f[tmp^1][j]+1,f[tmp][j]+1));
if(i==a[num].pos && !(m>a[num].l && m<a[num].h))
f[tmp][m]=inf+m;
for(int j=1; j<=m-down[i]; ++j)
{
f[tmp][j]=min(f[tmp][j],f[tmp^1][j+down[i]]);
if(i==a[num].pos && !(j>a[num].l && j<a[num].h))
f[tmp][j]=inf+m;
}
if(a[num].pos==i)
{
for(int j=a[num].l+1; j<a[num].h; ++j)
if(f[tmp][j]<inf)
{
k=num;
break;
}
num++;
}
}
}
inline void get_ans()
{
int tmp=n%2;
for(int i=1; i<=m; ++i)
ans=min(ans,f[tmp][i]);
}
int main()
{
scanf("%d%d%d",&n,&m,&t);
for(int i=1; i<=n; ++i)
scanf("%d%d",&up[i],&down[i]);
for(int i=1; i<=t; ++i)
scanf("%d%d%d",&a[i].pos,&a[i].l,&a[i].h);
sort(a+1,a+t+1,cmp);
dp();
get_ans();
if(ans<inf)
printf("1\n%d\n",ans);
else
printf("0\n%d\n",k);
return 0;
}
A、试题类型:
基本算法。
B、算法模型:
暴力枚举,搜索。
C、试题说明:
循环控制,划定范围。然后逐次枚举。
#include<cstdio>
using namespace std;
int d,n,a[300][300],cnt,maxm=-1,x,y,k;
int main()
{
scanf("%d%d",&d,&n);
for(int i=1;i<=n;i++)
{
scanf("%d %d",&x,&y);
scanf("%d",&a[x+20][y+20]);
}
for(int i=0+20;i<=128+20;i++)
for(int j=0+20;j<=128+20;j++)
{
int sum=0;
for(int u=i-d;u<=i+d;u++)
for(int v=j-d;v<=j+d;v++)
sum=sum+a[u][v];
if(sum==maxm)cnt++;
if(sum>maxm){maxm=sum; cnt=1;}
}
printf("%d %d",cnt,maxm);
return 0;
}
A、试题类型:
最短路径。
B、算法模型:
bfs。
C、试题说明:
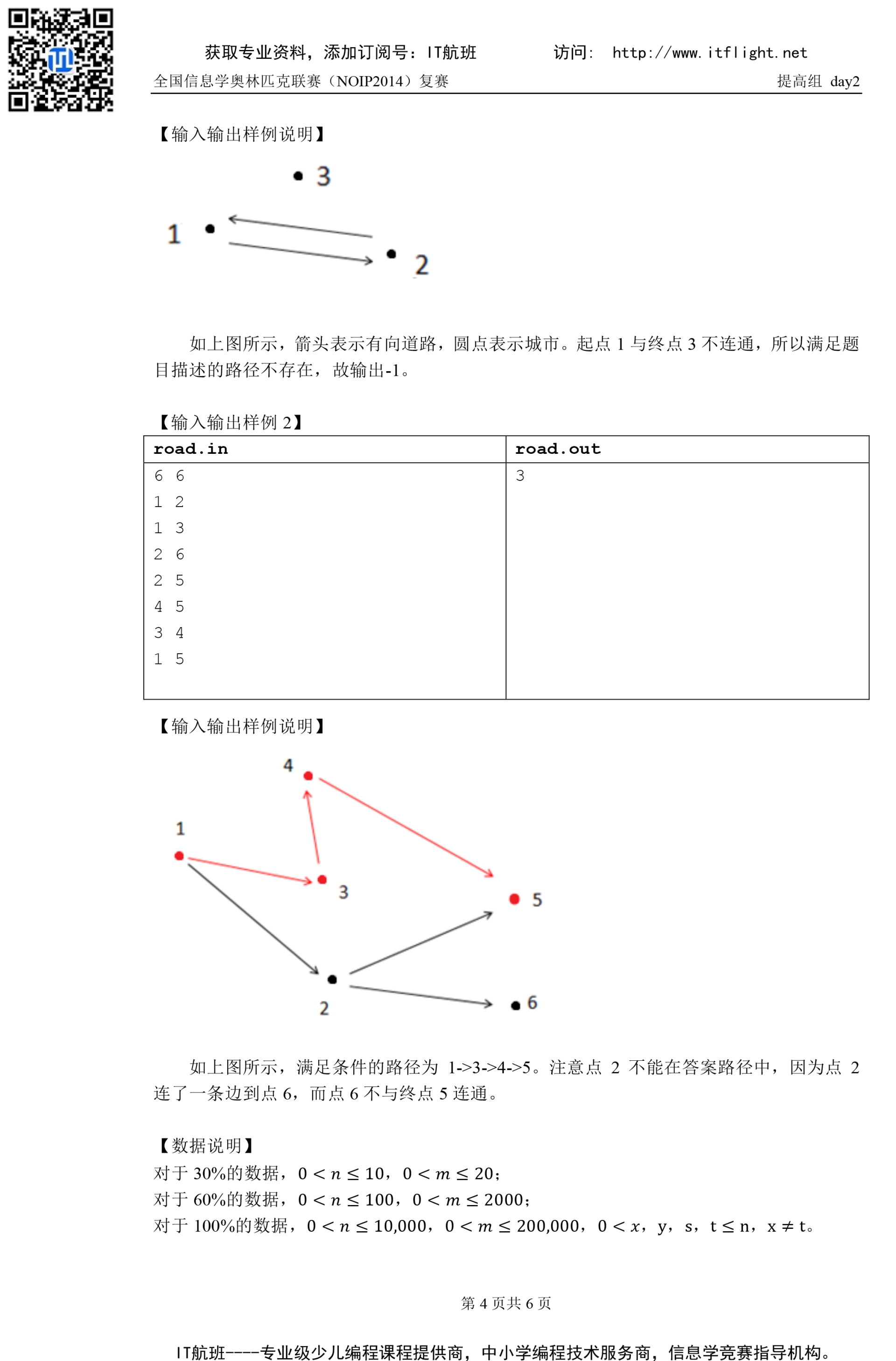
这里用 h1 储存所有边,h2 储存所有逆向边。
1、反向bfs一次,即可得到每个点能否到达终点 t,记为 flag[i]。
2、求 s 到 t 的最短路,由于每条边的长度都是1,可以直接采用bfs来做。
正向与逆向都可以。
#include<cstdio>
#include<cstring>
#include<cctype>
#include<algorithm>
using namespace std;
const int maxn=1e4;
int q[maxn+10];
bool flag[maxn+10],used[maxn+10];
struct tnode
{
int d;
tnode *next;
}*h1[maxn+10],*h2[maxn+10];
int getin()
{
int ans=0;
char tmp;
while(!isdigit(tmp=getchar()));
do ans=(ans<<3)+(ans<<1)+tmp-'0';
while(isdigit(tmp=getchar()));
return ans;
}
void add1(int u,int v)
{
tnode *p=new tnode;
(*p).d=v,(*p).next=h1[u],h1[u]=p;
}
void add2(int u,int v)
{
tnode *p=new tnode;
(*p).d=v,(*p).next=h2[u],h2[u]=p;
}
bool ok(int u)
{
if(!flag[u] || used[u])
return 0;
tnode *p=h1[u];
while(p)
{
if(!flag[(*p).d])
return 0;
p=(*p).next;
}
return 1;
}
int main()
{
int n,m,i,x,y,s,t,l,r,k,ans=0;
tnode *p;
n=getin(),m=getin();
for(i=1;i<=m;i++)
{
x=getin(),y=getin();
add1(x,y),add2(y,x);
}
s=getin(),t=getin();
l=r=1,q[1]=t,flag[t]=1;
while(l<=r)
{
p=h2[q[l]],l++;
while(p)
{
if(!flag[(*p).d])
q[++r]=(*p).d,flag[(*p).d]=1;
p=(*p).next;
}
}
if(!flag[s])
{
printf("-1\n");
return 0;
}
l=r=1,q[1]=t,k,used[t]=1;
while(l<=r)
{
for(i=l,k=r;i<=k;i++)
for(p=h2[q[i]];p;p=(*p).next)
{
if(!ok((*p).d))continue;
if((*p).d==s)
{
printf("%d\n",ans+1);return 0;
}
q[++r]=(*p).d,used[q[r]]=1;
}
l=k+1,ans++;
}
printf("-1\n");
return 0;
}
A、试题类型:
解方程 + 数论 + 模拟。
B、算法模型:
暴力,秦九韶。
C、试题说明:
题目大意:求一个多项式方程在[ 1 , m ] [1, m][1,m]的整数解。
要用到一个算法:秦九韶算法,就是减少多项式的计算次数。
然后暴力枚举[ 1 , m ] [1, m][1,m]。
由于系数太大,还要取模。将原数分别模多个质数,如果答案都为0是就可以近似认为是答案了。
满分做法:
注意到在模p意义下若f ( x ) = 0f。
则f ( x + k ∗ p ) = 0。
所以只用枚举到质数范围就行了。
#include<cstdio>
#include<cstring>
const int MOD[3] = {20029,22277,23333};
const int MaxMod = 3;
int n, m;
char ch[20001];
long long a[5][105];
int Mod[5][40001];
int ans[1000001];
inline void read(int i)
{
int f = 1; char ch = getchar();
while(ch < '0' || ch > '9')
{
if(ch == '-')
f = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9')
{
for(int t = 0; t < MaxMod; t++)
a[t][i] = (a[t][i] * 10 + ch - '0') % MOD[t];
ch = getchar();
}
if(f == -1)
for(int t = 0; t < MaxMod; t++)
a[t][i] = MOD[t] - a[t][i];
}
inline bool pd(int x, int t)
{
long long sum = a[t][n];
for(int i = n - 1; i >= 0; i--)
sum = (sum * x + a[t][i]) % MOD[t];
return sum == 0;
}
inline bool check(int x)
{
for(int t = 0; t < MaxMod; t++)
if(!Mod[t][x % MOD[t]])
return false;
return true;
}
int main()
{
scanf("%d%d", &n, &m);
for(int i = 0; i <= n;i++) read(i);
for(int t = 0; t < MaxMod; t++)//枚举MOD
for(int x = 1; x < MOD[t]; x++)//枚举x
if(pd(x, t))
Mod[t][x] = true;
for(int x = 1; x <= m; x++)
if(check(x))
ans[++ans[0]] = x;
printf("%d\n", ans[0]);
for(int i = 1; i <= ans[0]; i++)
printf("%d\n", ans[i]);
return 0;
}
IT航班提供:教辅资料、课程视频、课程书籍、竞赛辅导、少儿编程指导、课程采购、加盟、少儿编程资料、少儿编程课程、保送生、特长生、加分、中小学计算机教育、中小学信息学、竞赛、中小学信息学课程、人工智能、中小学编程加盟、少儿编程加盟、品牌加盟、技术加盟、技术指导、课程加盟、师资培训、中小学编程教辅资料、中小学编程教师培训、少儿编程教学书籍、少儿编程视频、教学书籍、教师培训、教学视频、CSP-J/S、中小学信息学课程服务、竞赛指导、课程提供、国内外计算机中小学计算机竞赛、信息学竞赛、信息学课程提供商、信息学奥林匹克。
IT航班支持----中小学编程比赛汇总:
第一部分:国内比赛(IT航班支持)
1、软件能力认证(CSP-JS)
2、全国青少年信息学奥林匹克联赛(NOIP)
3、全国青少年信息学奥林匹克竞赛(NOI)
4、中国青少年………………………
5、………………………创新挑战赛
6、全国青少年………………………
7、………………………
8、 恩欧希教育信息化发明创新奖
9、世界机器人大赛(WRC)
10、………………………大赛
11、少………………………智能教育成果展示大赛
12、“明天小小科学家”奖励活动
13、………………………
14、………………………
15、国际信息学………………………
16、………………………
第二部分:国际比赛(IT航班支持)
17、………………………
18、国际………………………
19、………………………
20、美国信息学………………………
21、加拿大………………………
22、官方邀请赛 (CCO)
23、国际计算思维………………………
24、美国计算机………………………
25、澳大利亚………………………
第三部分:企业比赛(IT航班支持)
26、微软MTA
27、………………………挑战赛
28、………………………科学奖
29、………………………学奖
30、………………………创新挑战赛
31、………………………挑战赛
32、………………………芯计算机表演赛
33、………………………大赛
第四部分:Scratch相关竞赛(IT航班支持)
34、全国中小学生电脑制作大赛
35、………………………
36、………………………
37、………………………
第五部分:其它(IT航班支持)
38、NOI夏令营
39、NOI冬令营(NOIWC)
40、全国青少年………………………
41、国际青少年………………………
联系方式:
A、官方网址:
B、微信公众号:
添加微信,获取资料。

关注公众号,获取动态。
