关键词:
北京中关村;海淀黄庄;北京大学;清华大学。少儿编程;中小学编程;信息学竞赛;计算机竞赛;NOIP;NOIP竞赛;CSP-J/S竞赛;NOI竞赛。北京中学;东坝。
2002年、普及组、复赛,第8届。
面向6-18岁中小学生,做最专业的中小学编程教育。


解析与答案:
A、试题类型:
数学与逻辑。
B、算法模型:
推导。
C、试题说明:
无。
#include <stdio.h>
#include <stdlib.h>
int main()
{
int n, k;
double s;
scanf("%d", &k);
s = 0.0;
n = 1;
while (1) //死循环
{
s = s + 1.0/n; //求s=1+1/2+...+1/n
if(s > k)
{
printf("%d\n", n);
break; //跳出死循环
}
n++;
}
return 0;
}
A、试题类型:
数字问题。
B、算法模型:
暴力枚举与DFS。
C、试题说明:
无。
#include <iostream>
#include<cstdio>
#define N 100000001
using namespace std;
int a[22]={0};
long long sum=0;
int num=0;
int n=0,k=0;
int ret=0;
bool ok(long long x)
{
if(x==2) return 1;
if(x%2==0) return 0;
for(int i=2;i*i<=x;i++)
{
if(x%i==0) return 0;
}
return 1;
}
void DFS(int pos)
{
if(pos==n+1)
{
if(ok(sum)) ret++;
return;
}
if(num+n-pos+1>k)
DFS(pos+1);
if(num>=k)
return;
sum+=a[pos];
num++;
DFS(pos+1);
sum-=a[pos];
num--;
}
int main()
{
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
DFS(1);
printf("%d\n",ret);
return 0;
}
A、试题类型:
基本数据结构。
B、算法模型:
DFS。
C、试题说明:
无。
#include <iostream>
#include <cstdio> //cstdio内有scanf()函数
#include <cstring> //cstring内有strlen(),memset()函数
using namespace std;
char num[32]; //字符型num数组用于输入做变换的巨大数字,它最多长达31位数
int value[32]={0,1}; //value[1]设为1,既是乘法的开始,也是k=0这种情况的特殊结果
int change[10][10]; //bool型的change[i][j]储存是否存在从i向j的变换
int node[10]; //bool型的node[n]记录n这种变换结果是否被记录过
int factor; //factor记录每一位上可能的变换结果的总数,所有位上的factor相乘得到的即是所求的种类总数
int multilen=1; //变化的multilen反映的是当前高精度乘法结果的位数
void DFS(int n) //深度优先搜索一个数字
{
int j;
if(node[n]) //如果node[n]为1,表示n这种变换结果已被记录过
return ; //这时再向下搜索得到的也只是与之前重复的情况,这时候就不必再DFS,只要返回上一个DFS(调用该DFS的DFS)
else //如果node[n]为0,表示n这种结果没有被记录过
{
node[n]=1; //下面要记录它,将node[n]设为1
factor++; //用全局变量factor因子记录这种情况
}
for(j=0;j<=9;j++) //对于这10个数字j
if(change[n][j]) //如果存在从n向j的变换
DFS(j); //那么就变换,搜索变换后的j
}
void multiply() //高精度乘法,将因子factor乘入数组value[]
{
int carry=0; //carry表示每次乘法需要进位的数字
for(int i=1;i<=multilen;i++) //从第一位到最后一位每一位都要乘
{
value[i]=value[i]*factor+carry; //乘上因子factor,再加上上一位留下的进位数carry
carry=value[i]/10; //carry再变成当前这一位对下一位产生的进位数
value[i]%=10; //进位后,本位当然要对10取余
}
if(carry>0) //如果到最后一位也乘完,还存在向下一位的进位数carry
value[++multilen]=carry; //那么总位数就要增加一位,并将进位数放进去
}
int main()
{
int k,i,j,length; //length将储存num的长度
scanf("%s%d",num,&k); //用scanf以跳过空格
memset(change,0,sizeof(change)); //change[i][j]为0时表示不存在从i向j的变换,先清零,再在后面赋1
while(k--)
{
cin>>i>>j;
change[i][j]=1; //change[i][j]为1时表示存在从i向j的变换
}
length=strlen(num); //这样做仅避免反复的求长度运算
for(i=0;i<length;i++) //遍历输入数字的每一位数
{
memset(node,0,sizeof(node)); //每次将DFS节点数组node[]清空
factor=0; //factor临时储存每一位的因子
DFS(num[i]-'0'); //对每一位深度优先搜索能做多少次变换
multiply(); //将因子相乘(高精度)放入数组value[]
}
for(i=multilen;i>=1;i--)
cout<<value[i]; //从高位到低位输出每一位数
return 0;
}
A、试题类型:
棋盘问题。
B、算法模型:
多方程问题。
C、试题说明:
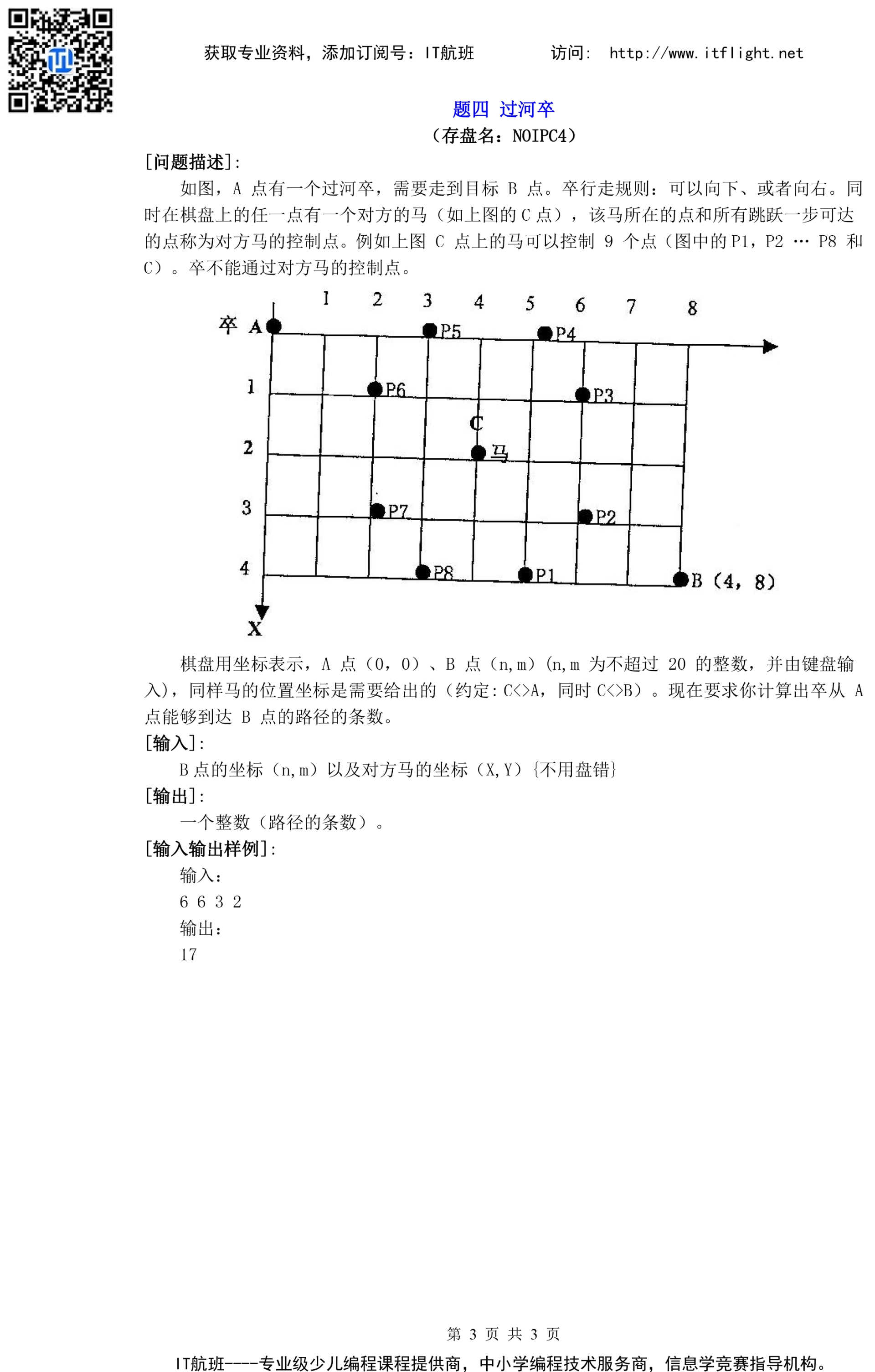
要到达棋盘上的一个点,只能从左边过来或是从上面下来。
根据加法原理,到达某一点的路径数目,等于到达其相邻上,左两点的路径数目之和。
可以使用逐列(或逐行)递推的方法,求出从起始顶点到重点的路径数目,即使有障碍(将马的控制点称为障碍),这一方法也完全适用,只要将到达该点的路径数目置为0即可,用F[i,j]表示到达点(i,j)的路径数目,g[i,j]表示点(i,j)有无障碍。
递推方程如下:
F[0,0] = 1
F[i,j] = 0 { g[x,y] = 1 }
F[i,0] = F[i-1,0] {i > 0,g[x,y] = 0}
F[0,j] = F[0,j-1] {j > 0,g[x,y] = 0}
F[i,j] = F[i-1,j] + F[i,j-1] {i > 0,j > 0,g[x,y] = 0}
要考虑精度问题,当n,m都很大时,可能会超过MaxLongInt,要使用Comp类型计数(Comp类型已经足够了,即使n=20,m=20,没有任何障碍的情况下的结果也只有14,5位的样子)。
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=120;
int t=10;//fang zhi tiao dao fu shu
long long dp[N][N],b[N][N],c[N][N],n,m,x,y;
inline void read(long long & x)
{
char c=getchar();
x=0;
while(c<'0'&&c>'9')c=getchar();
while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar();
}
int main()
{
read(n);
read(m);
read(x);
read(y);
c[x+t][y+t]=1;
c[x-2+t][y+1+t]=1;
c[x+2+t][y+1+t]=1;
c[x-1+t][y+2+t]=1;
c[x+1+t][y+2+t]=1;
c[x-2+t][y-1+t]=1;
c[x+2+t][y-1+t]=1;
c[x-1+t][y-2+t]=1;
c[x+1+t][y-2+t]=1;
dp[t][t-1]=1;
for(int i=t;i<=n+t;i++)
{
for(int j=t;j<=m+t;j++)
{
if(c[i][j]!=1)
{
dp[i][j]=dp[i-1][j]+dp[i][j-1];
}
}
}
printf("%lld",dp[t+n][t+m]);
return 0;
}
IT航班提供:课程视频、、课程书籍、竞赛辅导、少儿编程指导、课程采购、加盟、少儿编程资料、少儿编程课程、保送生、特长生、加分、中小学计算机教育、中小学信息学、竞赛、中小学信息学课程、人工智能、中小学编程加盟、少儿编程加盟、品牌加盟、技术加盟、技术指导、课程加盟、师资培训、中小学编程教辅资料、中小学编程教师培训、少儿编程教学书籍、少儿编程视频、教学书籍、教师培训、教学视频、CSP-J/S、中小学信息学课程服务、竞赛指导、课程提供、国内外计算机中小学计算机竞赛、信息学竞赛、信息学课程提供商、信息学奥林匹克。
IT航班支持----中小学编程比赛汇总:
第一部分:国内比赛(IT航班支持)
1、软件能力认证(CSP-JS)
2、全国青少年信息学奥林匹克联赛(NOIP)
3、全国青少年信息学奥林匹克竞赛(NOI)
4、中国青少年………………………
5、………………………创新挑战赛
6、全国青少年………………………
7、………………………
8、 恩欧希教育信息化发明创新奖
9、世界机器人大赛(WRC)
10、………………………大赛
11、少………………………智能教育成果展示大赛
12、“明天小小科学家”奖励活动
13、………………………
14、………………………
15、国际信息学………………………
16、………………………
第二部分:国际比赛(IT航班支持)
17、………………………
18、国际………………………
19、………………………
20、美国信息学………………………
21、加拿大………………………
22、官方邀请赛 (CCO)
23、国际计算思维………………………
24、美国计算机………………………
25、澳大利亚………………………
第三部分:企业比赛(IT航班支持)
26、微软MTA
27、………………………挑战赛
28、………………………科学奖
29、………………………学奖
30、………………………创新挑战赛
31、………………………挑战赛
32、………………………芯计算机表演赛
33、………………………大赛
第四部分:Scratch相关竞赛(IT航班支持)
34、全国中小学生电脑制作大赛
35、………………………
36、………………………
37、………………………
第五部分:其它(IT航班支持)
38、NOI夏令营
39、NOI冬令营(NOIWC)
40、全国青少年………………………
41、国际青少年………………………
联系方式:
A、官方网址:
B、微信公众号:
添加微信,获取资料。

关注公众号,获取动态。
